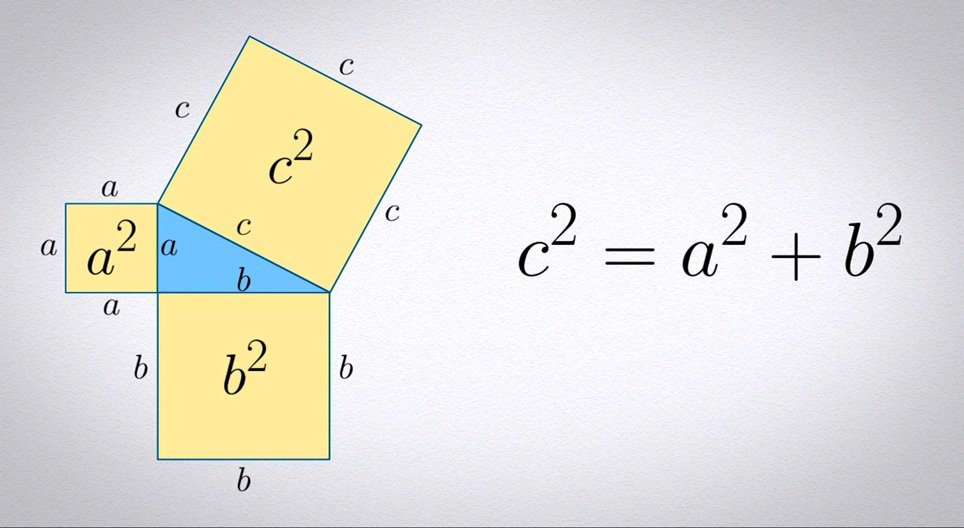Теорема Піфагора є однією з найвідоміших у математиці. Вона пояснює зв’язок між сторонами прямокутного трикутника. Формула теореми допомагає розв’язувати безліч практичних завдань у геометрії, архітектурі, фізиці та навіть у повсякденному житті.

Що таке теорема Піфагора?

Теорема Піфагора стверджує, що у будь-якому прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Це означає, що якщо позначити сторони як a і b (катети), а гіпотенузу як c, то виконується формула:
a² + b² = c².

Хто відкрив теорему Піфагора?

Теорема Піфагора названа на честь давньогрецького математика Піфагора. Він жив у VI столітті до нашої ери і заснував школу, де вивчали гармонію чисел, музику та геометрію. Хоча подібні знання існували ще у Вавилоні та Єгипті, саме Піфагор систематизував і довів цю теорему.

Як виглядає прямокутний трикутник?

Прямокутний трикутник має один кут рівний 90°. Дві сторони, що утворюють цей кут, називаються катетами. Сторона навпроти прямого кута – гіпотенуза. Теорема Піфагора допомагає знайти її довжину або довжину одного з катетів, якщо відомі інші.

Чому теорема Піфагора важлива?

Теорема Піфагораа важлива, бо вона універсальна. Її застосовують у кресленні, будівництві, інженерії, фізиці та навіть у комп’ютерній графіці. Завдяки їй можна обчислити відстань між точками, перевірити правильність побудови або створити точні пропорції.

Формула теореми Піфагора

Формула виглядає дуже просто:
a² + b² = c².
Вона дозволяє швидко виконати обчислення. Наприклад, якщо катети дорівнюють 3 і 4, то гіпотенуза буде:
c² = 3² + 4² = 9 + 16 = 25, отже c = 5.

Докази теореми Піфагора

Теорема Піфагораа має понад 370 різних доказів. Вони включають алгебраїчні, геометричні та навіть механічні пояснення. Наприклад, один з найвідоміших – це побудова квадратів на сторонах трикутника і доведення, що площа великого квадрата дорівнює сумі двох менших.

Геометричний доказ теореми Піфагора

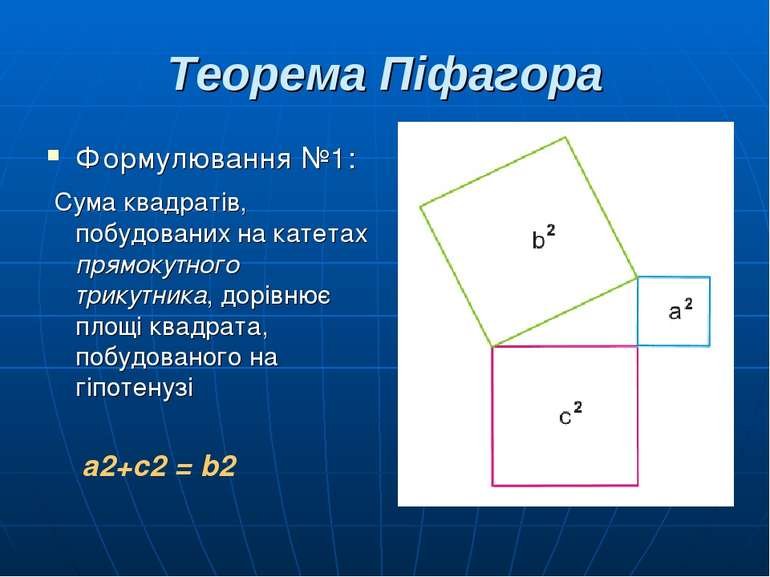
Геометричний доказ базується на малюнку з квадратом, усередині якого розташовані чотири однакових прямокутних трикутники. Коли їх скласти по-іншому, видно, що площа великого квадрата дорівнює сумі квадратів катетів. Це наочне пояснення дуже зручне для школярів.

Алгебраїчний доказ теореми Піфагора

Алгебраїчний доказ використовує рівняння і розкладання виразів. Якщо побудувати квадрат зі стороною (a + b), то його площа можна обчислити двома способами. Порівнюючи ці площі, легко отримати формулу a² + b² = c². Це доводить істинність теореми.

Теорема Піфагораа і координатна геометрія

У координатній геометрії теорема Піфагораа допомагає знаходити відстань між двома точками. Формула виглядає так:
d = √((x₂ – x₁)² + (y₂ – y₁)²).
Вона є прямим наслідком класичної формули a² + b² = c².

Теорема Піфагора в архітектурі

Архітектори часто застосовують теорему Піфагора, щоб будувати прямі кути, розраховувати пропорції та перевіряти точність креслень. Відомий приклад – будівництво пірамід у Єгипті, де робітники використовували подібні принципи для визначення правильних кутів.

Теорема Піфагораа у фізиці

У фізиці теорема Піфагора застосовується для обчислення результуючої сили, швидкості або переміщення. Наприклад, коли тіло рухається одночасно вгору і вперед, його траєкторія визначається саме за допомогою цієї формули.аУ фізиці теорема Піфагора застосовується для обчислення результуючої сили, швидкості або переміщення. Наприклад, коли тіло рухається одночасно вгору і вперед, його траєкторія визначається саме за допомогою цієї формули.

Теорема Піфагораа у повсякденному житті

Теорема Піфагораа корисна у побуті. Вона допомагає знайти найкоротший шлях, розрахувати довжину драбини чи кабелю, визначити відстань між будинками на карті. Люди часто користуються нею, навіть не підозрюючи, що застосовують математичну теорему.

Приклади розв’язування задач

Приклад 1. Якщо катети дорівнюють 6 і 8, то гіпотенуза:
c² = 6² + 8² = 36 + 64 = 100, отже c = 10.

Приклад 2. Якщо гіпотенуза 13, а один катет 5, то другий:
b² = 13² – 5² = 169 – 25 = 144, отже b = 12.

Теорема Піфагора і трикутники Піфагора

Існують спеціальні цілі числа, які утворюють прямокутні трикутники. Наприклад, (3, 4, 5) або (5, 12, 13). Вони називаються піфагоровими трійками. Вони часто зустрічаються в задачах і роблять розрахунки простішими.

Теорема Піфагора і історія науки

Історія науки показує, що теорема Піфагораа відома більше 2500 років. Вона надихала математиків різних культур – від Вавилону до Індії та Китаю. Завдяки їй розвивалась геометрія, тригонометрія і навіть астрономія.

Теорема Піфагора і сучасні технології

Сучасні технології теж використовують цю формулу. Наприклад, GPS-навігатори розраховують відстань між точками за допомогою неї. Комп’ютерна графіка та 3D-моделювання базуються на обчисленнях, які випливають із цієї теореми.

Висновок

Теорема Піфагора – це не просто формула з підручника. Це універсальний інструмент, який поєднує геометрію, фізику, архітектуру та сучасні технології. Вона доводить, що математика є фундаментом нашого світу.

Читати далі: Пробне ЗНО 2025 – Повний гід для успішного тестування

Часті запитання про теорему Піфагора